Énoncé   

Examinez cette image comportant 15 nains. Elle est découpée en 3 parties.

Lorsque l'on inverse les 2 parties du haut, on n'a plus que 14 nains :

Où a disparu le nain manquant ? (La seconde image est vraiment issue de la première par simple inversion des deux parties du haut, il n'y a pas d'arnaque de ce genre.)

   Solution   

Tout d'abord, ce dont il faut bien se convaincre, c'est qu'il n'y a vraiment pas de tricherie : on obtient bien l'une des deux images en échangeant les parties hautes de l'autre.

Donc la "surface" de nains est la même (surface en pixel par exemple), l'astuce est dans le réarrangement des parties hautes et des basses pour afficher un nain de moins. Les nains de la seconde image seront donc plus grands (en hauteur) que ceux de la première.

Identifions les hauts de nains par des nombres et les bas par des lettres comme indiqué sur les figures 1 et 2 :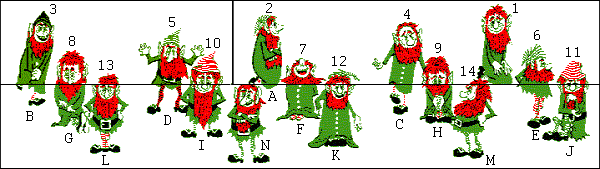

Figure 1 : les 15 nains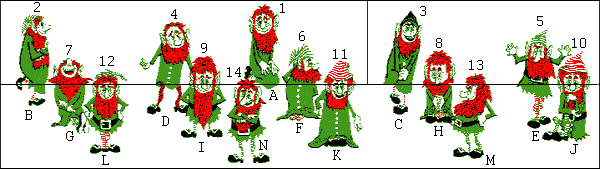


Figure 2 : les 14 nains

Voyons le nains 1 de la figure 1 : il n'a pas de bas, alors que sur la figure 2, le bas A lui est adjoint : il est donc déjà plus grand. Mais d'où vient ce bas A ? Il était accolé au haut 2 sur la figure 1. Ce haut 2 perd donc le bas A, mais obtient la bas B sur la figure 2 : ce nain est plus grand. Le bas B était avec le haut 3 qui lui obtient le bas C : le nain grandit. Etc.

On peut continuer ainsi dans l'ordre des numérotations jusqu'au bas N qui n'avait pas de haut et qui obtient le haut 14 (ce qui pourrait être la houppette de N sur la figure 1 n'est que le pied du 2).

Pour finir de comprendre, classons maintenant les hauts et les bas par ordre de taille, représentons-les sous forme de barres verticales (finalement, à la lecture de ce qui précède, on voit que seule la hauteur compte) et mettons-les les uns au dessus des autres tels qu'ils apparaissent sur la figure 1. On obtient la figure 3 :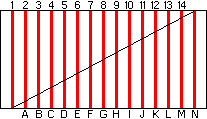

Figure 3

Le haut 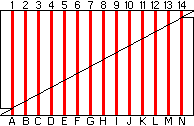1 n'a pas de bas (comme indiqué précédemment), 2 avec A, 3 avec B ... 14 avec M et enfin N tout seul. Donc 15 nains. Si on effectue le glissement du triangle du bas d'une unité vers la gauche, on obtient la figure 4 :

Figure 4

On remarque que l'on obtient exactement les arrangements de la figure 2 : 1 avec A, 2 avec B ... 14 avec N. Donc 14 nains.

Pour conclure, pas de disparition, mais un réarrangement des parties hautes et des parties basses.

Ne vous inquiétez pas : les billets de banque sont prévus pour prévenir ce genre d'astuce ... :-)